Map projections

We can record locations out in the field using Latitude-Longitude, but it’s not possible to use angular coordinates to draw geospatial features on a flat map or screen. For this, we need to use Cartesian coordinates, plus a map projection to convert between the angular and Cartesian coordinates. Together, these form a projected SRS

Some more phrases to add to our GIS vocabulary:

Cartesian coordinates

Coordinates on a flat plane with the X and Y axes at 90°. For most map projections, these coordinates will be measured in metres from a 0,0 reference point where the X and Y axes intersect. The real-world location of the 0,0 point depends on the map projection

Map projection

A map projection is a mathematical formula to convert between coordinate systems. It is used to draw features on the curved surface of the earth on a flat piece of paper or screen whilst maintaining accurate spatial releationships between those real-world features

Imagine that the earth is a football You want to lay the surface of the football flat, but the only way to do this is to tear it into pieces, and then ideally stretch some areas and squash others so that the fabric lies flat. This would, of course, break up or distort any pictures drawn on the surface of the football. Likewise, all map projections introduce some degree of distortion - this is inevitable

To help you picture how a map projection works, imagine that there is a light bulb at the centre of the earth. When we hold a piece of paper against the earth’s surface, our flat map is formed by the shadows cast onto the paper. We can hold the paper flat, just touching the earth at a tangent (azimuthal projection), causing greater distortion the further we move from the place where the paper touches the earth. Or we can wrap the paper around the globe in a cone (conic projection) or cylinder (cylindrical projection) to draw on the earth’s surface, before unrolling the paper to flat:

Many map projections have been developed through the history of cartography. Some map projections are designed to accurately represent only small areas of the earth’s surface, while others attempt to minimise certain types of distortion, for example maintaining the correct area of land masses, or the correct distance between cities

Remember that you can always look up these technical terms for a different way of explaining them, or more detail

• Wiki GIS glossary
• ESRI GIS dictionary

To see the effect of your choice of map projection on a country’s apparent shape and size:

1. Choose a map projection from the dropdown list
2. Click on a country in either map

Change the project-wide CRS in QGIS

We use the term SRS to emphasise the need for information on the datum (see next page) as well as the map projection. However, QGIS uses the term CRS, or Coordinate Reference System

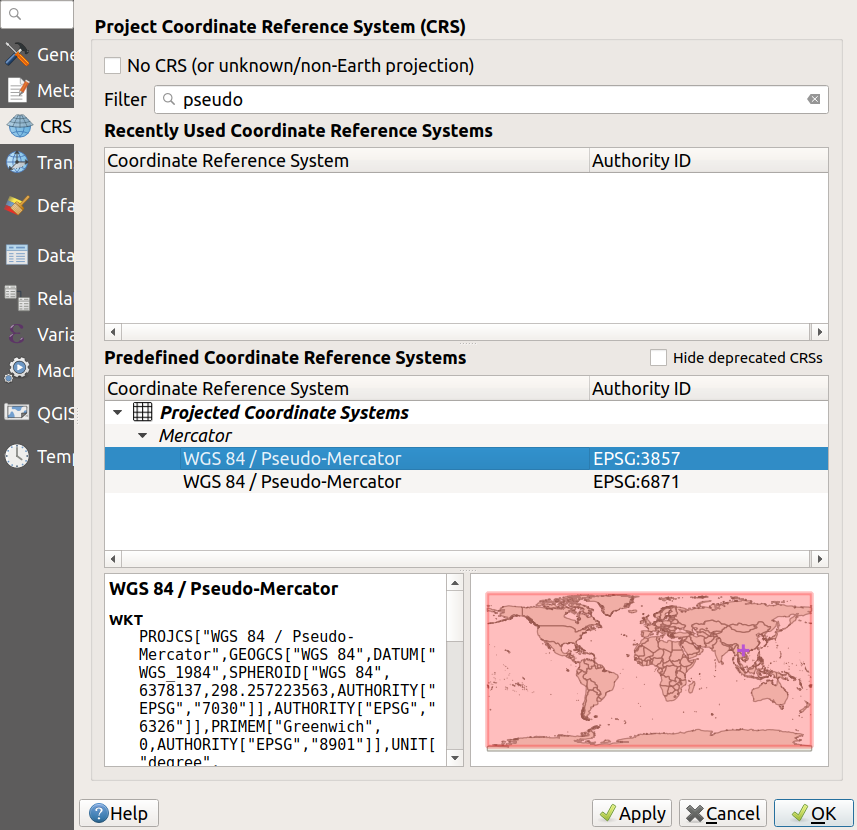
Up until now, we’ve been using Latitude-Longitude (EPSG code 4326) as our project-wide CRS, but it’s possible to change this. Let’s switch to a projected SRS, specifically Pseudo-Mercator (EPSG code 3857), as used by OpenStreetMap, Google maps, Bing etc

Be aware that you should always choose a project CRS that is appropriate to the location and extent of your datasets, i.e. a global CRS for a global dataset, or you may get unexpected behaviour or cause QGIS to crash! Changing to a local/national CRS may also affect QGIS’ ability to draw the OpenStreetMap basemap

1. Click on the Project CRS button in the bottom right of the QGIS window - refer to the QGIS Desktop page in the Introduction module if you can’t remember where this is
2. When the Project Properties - CRS window opens, type pseudo into the search box at the top, and select WGS 84 / Pseudo Mercator in the Predefined Coordinate Reference Systems box in the centre
   Screenshot

   
3. Click OK and note how the EPSG code to the bottom right has changed from 4326 to 3857
4. Move your mouse over the map, and see how the coordinates in the Mouse coordinates area of the QGIS window (bottom centre) are now much larger numbers

---